Logistic Regression using Python

Last Updated : 10 Feb, 2026

Logistic Regression is a widely used supervised machine learning algorithm used for classification tasks. In Python, it helps model the relationship between input features and a categorical outcome by estimating class probabilities, making it simple, efficient and easy to interpret.

  • Used for binary and multiclass classification
  • Predicts probabilities using the logistic (sigmoid) function
logistic_regression_making_decisions
Logistic Regression

We will build a classifier that predicts whether a tumour is malignant or benign, based on medical measurements using Python.

Step 1: Import Required Libraries

Python 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix,precision_score, recall_score,f1_score,roc_curve, roc_auc_score

Step 2: Load the Dataset

This step loads the Breast Cancer dataset from scikit learn. The dataset is provided as a structured object that bundles everything needed for a classification task. It contains:

  • Feature matrix: Numerical measurements used as input to the model
  • Target labels: The class to predict
  • Feature names: Descriptions of each input feature
  • Metadata: Additional information about the dataset

This structure makes the dataset easy to explore, preprocess and use directly for model training.

Python 
data = load_breast_cancer()

Step 3: Convert Data to a Pandas DataFrame

The raw dataset is converted into pandas structures for easier handling and analysis. Using a DataFrame improves readability, supports exploratory data analysis and aligns with real world data workflows commonly used in production.

  • X represents the input features
  • y represents the target variable
Python 
X = pd.DataFrame(data.data, columns=data.feature_names)
y = pd.Series(data.target)

Step 4: Train and Test Split

This step splits the data into training and testing sets. Here we will use 25% of data for testing and rest for training.

Python 
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=29
)

Step 5: Feature Scaling

This step standardizes feature values so they are on a similar scale. Logistic Regression uses gradient based optimization which is sensitive to feature magnitudes, so scaling helps the model train correctly. The scaler is fit only on training data and then applied to test data to avoid data leakage.

Python 
scaler = StandardScaler()

X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Step 6: Train the Logistic Regression Model

This step trains the Logistic Regression model on the scaled training data. Here:

  • The model learns feature weights that separate the classes,
  • Applies the sigmoid function to compute probabilities.
  • Assigns a class based on those probabilities.
Python 
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)

Step 7: Make Predictions

At this stage, the trained model is used to make predictions on unseen test data. It computes probabilities for each class and applies a threshold (default = 0.5) to convert them into class labels.

  • 1: Predicted as benign
  • 0: Predicted as malignant
Python 
y_pred = model.predict(X_test)
y_pred

Output:

Output-LR
Predicted Labels

Step 8: Model Evaluation

At this stage, predictions are available. We now evaluate how well the model performs using multiple metrics, since each metric highlights a different aspect of performance.

Accuracy Score

Accuracy measures how often the model makes correct predictions overall.

  • Gives a quick idea of overall correctness
  • Works well when classes are balanced
  • Can be misleading for imbalanced datasets
Python 
accuracy = accuracy_score(y_test, y_pred)
print(f"accuracy: {round(accuracy,2)}")

Output:

accuracy: 0.98

Confusion Matrix

A confusion matrix shows where the model is right and where it makes mistakes by comparing predicted labels with actual labels.

  • Shows exact error types, not just a score
  • Helps understand false positives vs false negatives
  • Critical in domains like healthcare, where mistakes have different costs
Python 
cm = confusion_matrix(y_test, y_pred)
cm

Output:

Confusion-matrix
Confusion Matrix

Precision Score

Precision shows how many predicted positives are actually correct.

  • Focuses on reducing false positives
  • Important when wrong positives are costly
  • Commonly used in spam and fraud detection
Python 
precision = precision_score(y_test, y_pred)
f"Precision: {round(precision,2)}"

Output:

Precision: 0.99

Recall Score

Recall measures how many actual positives the model correctly identifies.

  • Focuses on reducing false negatives
  • Important when missing positives is risky
  • Used in healthcare and safety systems
Python 
recall = recall_score(y_test, y_pred)
f"Recall: {round(recall,2)}"

Output:

Recall: 0.98

F1 Score

F1 score balances precision and recall into a single metric.

  • Useful when data is imbalanced
  • Penalizes extreme precision or recall values
  • Preferred when both false positives and false negatives matter
Python 
f1 = f1_score(y_test, y_pred)
f"f1 score: {round(f1,2)}"

Output:

f1 score: 0.98

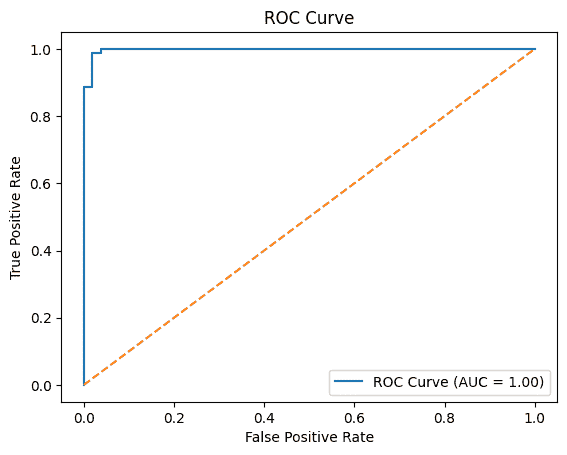
ROC-AUC Score

ROC-AUC shows how well the model separates classes across thresholds.

  • Measures ranking ability, not exact predictions
  • Higher value means better class separation
  • Works well for comparing classification models
Python 
y_prob = model.predict_proba(X_test)[:, 1]

fpr, tpr, thresholds = roc_curve(y_test, y_prob)

roc_auc = roc_auc_score(y_test, y_prob)

plt.figure()
plt.plot(fpr, tpr, label=f"ROC Curve (AUC = {roc_auc:.2f})")
plt.plot([0, 1], [0, 1], linestyle="--") 
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("ROC Curve")
plt.legend()
plt.show()

Output:

ROC-AUC-curve
ROC-AUC Curve

You can download the python notebook from here

Comment

Explore